A little while ago my friend William proposed a game that I thought was cute, and there turned out to be a pretty satisfying answer to the question of which player has a winning strategy. I figured that now that this blog exists, this could be a fun place to write up the story.

I remember the first time someone told me about game theory, they used as a starting example something like the following:

Two players take turns removing stones from a pile of $n$. On your turn you can remove between $1$ and $4$ stones, and you win if you remove the last one. Who wins?

The answer is that the first player can win if and only if the starting value of $n$ is not a multiple of 5. When you start your turn and $n$ is a multiple of 5, no matter what number $x$ of stones you pick, your opponent can respond by taking $5-x$ stones, leaving you once again with a multiple of 5 on your next turn. When the pile finally gets down to only 5 stones, you have no way of preventing your opponent from winning.

This game is essentially a variant of Nim (as I suppose are all impartial games – odds are pretty good that I type up an explanation of the Sprague-Grundy theorem as a blog post at some point), and is a nice introduction to combinatorial games because it has such a straightforward winning strategy. But William proposed a different version of the game: what if, instead of choosing a number between $1$ and $4$ of stones to remove, the number of allowed stones changed over time? Specifically,

An instance of the game is generated by randomly shuffling a set of cards labeled $1$ through $n$. Both players know the full outcome of the shuffle. On your turn, if the current top card of the deck is $k$, you can choose to remove between $1$ and $k$ cards from the top, and you win if you remove the last one. What’s the probability that this shuffling produces a winning game state for the first player?

Here, coming up with the right strategy feels less much less obvious – it seems like depending on what exactly the shuffling looks like, the right decisions to make could be very different. And indeed, I don’t know that there’s a simple characterization of what the optimal strategy is. However, it’s not too hard to characterize what the winning probabilities look like, at least asymptotically in $n$.

Player 1 has a winning strategy with probability $1 - \mathcal{O}\left(\sqrt{\frac{\log n}{n}}\right)$

Let me show you a situation I claim is really really good for player 1:

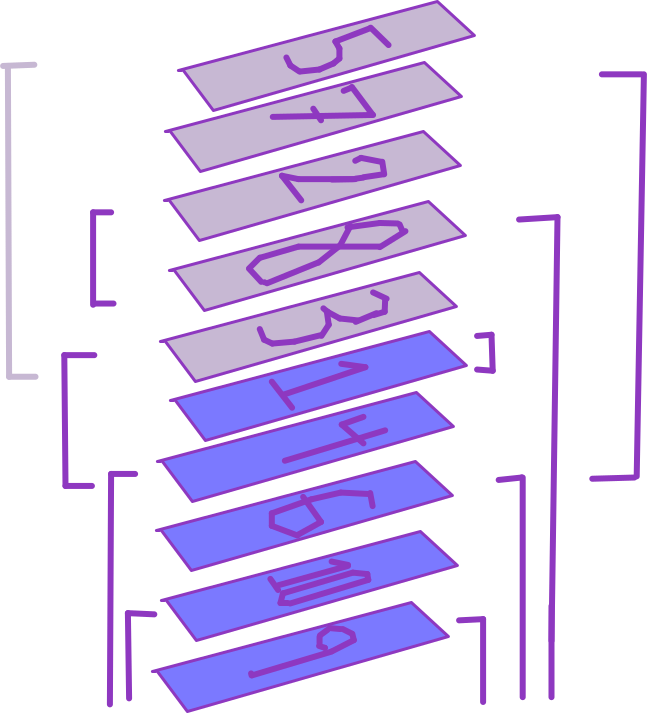
Example game
Grey cards indicate ones player 1 can take on her first turn.

In this picture, she can choose to remove up to any of the grey cards. Suppose she chose to remove only the first two.

Example game
Either of the two things player 2 could do in this configuration, player 1 could also have done on her first move.

Now, player 2 has very few options on his turn. In particular, the options available to player 2 are a strict subset of those that were available to player 1 on her turn. That means that, if player 2 has some strategy to let him win the game from this position, then actually player 1 could have used that strategy instead. (For example, in this case, if player 2 thought that taking the top 1 card in this position would put him into a winning state, then player 1 could have actually started by taking the top 3 cards instead of 2, and now she’d be winning.) This is called a “strategy stealing argument” – note that it doesn’t actually tell us what the right strategy is, it just shows that there must exist one that makes player 1 win.

By looking for configurations like this, we can give a lower bound on the probability that player 1 has a winning strategy in this game. Consider the probability that both of the following events happen:

  • The number on the top card is larger than $2\sqrt{n\log n}$
  • Among the first $\sqrt{n\log n}$ cards, there exists one whose number is less than $\sqrt{n \log n}$

The first of these events occurs with probability $1 - \frac{2\sqrt{n\log n}}{n} = 1 - 2\sqrt{\frac{\log n}{n}}$. For the second event, note that, although the numbers on the first $\sqrt{n \log n}$ cards aren’t actually independent, they’re basically independent – $\sqrt{n \log n}$ is such a small fraction of the deck that we aren’t changing the distribution of cards very much, so we can pretend we were drawing with replacement. Now, the probability of all of the first $\sqrt{n \log n}$ cards having value more than $\sqrt{n \log n}$ is $\left( 1 - \frac{\sqrt{n \log n}}{n} \right)^{\sqrt{n \log n}}$. As $n$ gets large, we can approximate this as $e^{- \log n} = \frac{1}{n}$. So, the probability that both events occur is $\left(1 - 2\sqrt{\frac{\log n}{n}}\right)\left(1 - \frac{1}{n}\right) = 1 - \mathcal{O}\left(\sqrt{\frac{\log n}{n}}\right)$. Whenever both of these events occur, we’ll have the same strategy-stealing setup as in the example: player 1 can force player 2 into a position where his options are a strict subset of what hers were initially. This argument tells us that the chances of player 2 winning the game go to zero as $n$ gets big – and in particular, go to zero almost as fast as $\frac{1}{\sqrt{n}}$. Using the same sort of argument again, we can also show that player 2’s winning probabilities don’t decay much faster than that – $\frac{1}{\sqrt{n}}$ is pretty much the right answer1.

Player 2 has a winning strategy with probability $\Omega\left( \sqrt{\frac{1}{n}} \right)$

Consider the probability that all of the following events happen:

  • The number on the first card is smaller than $\sqrt{n}$
  • The second through $\sqrt{n}$th card all have values at least $3\sqrt{n}$
  • Among the $\sqrt{n}$th through $2\sqrt{n}$th cards, all have value at most $\sqrt{n}$

This sequence of events means that, no matter what player 1 does, player 2 will then be in a position to do a strategy stealing. By a similar argument to above, these events occur with probability roughly $\left( \frac{1}{\sqrt{n}} \right)\left( e^{-1} \right) \left( e^{-1/3} \right) = \Omega\left( \sqrt{\frac{1}{n}} \right)$.

Other questions

This was a quick example of a case where a strategy stealing argument one step away let me characterize the winning probability of a game pretty tightly. If you thought this game sounded interesting, here’s a couple other questions that could be fun to think about:

  1. How do winning probabilities for this game work if, instead of shuffing cards $1$ through $n$, the card values are dice rolls (i.e. independent uniform values from 1 to 6)2? Strategy stealing tells us both players have a constant winning probability, but how do we figure out what that constant is?
  2. What about if the players don’t know the whole shuffling – i.e. they can only see the first card, so they’re playing with partial information and trying to maximize winning probability? Intuitively, you’d expect that when you shuffle $1$ through $n$, the right strategy might be to only take one card at a time at the beginning, because the fewer cards that are left the more chance your opponent instawins on the next turn. When the values are from dice rolls, you can write down some recurrences and you’ll start to see patterns.
  3. You could also define a variant of this game where, instead of removing cards from a stack, you lay out all the cards in a line. Now, on your turn, you can jump to a card up to as many steps away as the current value, where it then becomes the next player’s turn. You can never revisit an already visited card, and your goal is to never get stuck with no moves available to you. Who wins? None of the strategy stealing stuff works anymore, because now there’s some dependence on history. It seems likely that in the $1$ through $n$ shuffle case you almost never get stuck until the end, but maybe this game is fun for smaller cards? I haven’t thought much about it – let me know if you do!
Example game
Grey cards indicate ones that are available to move to on this turn; solid (think: face-down) cards indicate the already-visited ones.

  1. This $\sqrt{\log n}$ factor is a bit annoying – I suspect you could make it go away if you were a little more careful with things, but I’m just leaving this a rough sketch. ↩

  2. Or iid from some other distribution, say. The reason this approach was so strong here was because the card values were allowed to be really large, so it was likely to be able to pull these shenannigans – when cards have smaller numbers I expect it’ll be a much trickier problem. ↩