The Parable of the Underprepared Rock-Paper-Scissors Player

Last year, the floor I live on in Next House held a rock-paper-scissors competition. I got out in the first round (it turns out the “always do scissors because scissors is the best” strategy I’ve been using for the past ~6 years maybe doesn’t hold up against tournament play), but the person who ended up winning had an interesting strategy: he’d randomly generated a sequence of moves beforehand, and then just memorized and played those. This approach is attractive because it guarantees you’ll win with exactly 50-50 probability – there’s no danger of your opponent somehow figuring out and exploiting patterns in your behaviour (like they could for me)¹.

But there’s a² question you might worry about: what if, when you got to the tournament, you realized that it was more rounds than you’d expected, and you don’t have a long enough list of random moves prepared? You could just flip a coin to come up with some new ones – but, oh no, you left your coin at home. You could say “I’ll play according to my memorized moves until they run out, and then switch to my old deterministic strategy after that” – but if your opponents know your old deterministic strategy (e.g. if it’s just to always do scissors), they’ll totally destroy you at that point. You’re in a pretty bad pickle – somehow, you need to take the 100 random numbers you came with and turn them into 200 random numbers, without flipping any more coins.

“That sounds impossible!”, you cry in despair. “There’s just not enough entropy – there were only $3^{100}$ possibilities for the random move sequence I prepared, and I need to make it look like I’ve chosen a uniformly random element from a set of size $3^{200}$. No matter what approach I use to stir up this randomness, the distribution I output is necessarily going to be really far from the one I want.”

And of course, you’re completely correct. Assuming your opponents know what strategy you’re gonna use to mess up your random bits, it’s always going to be in principle possible for them to destroy you. Fortunately, though, in the real world you know that your adversaries are mere mortals. Even if they in theory have enough information to outplay you, that doesn’t mean that they’ll be able to figure out how to do so. This is the fundamental idea behind all of cryptography: when you can’t make something literally impossible, maybe you can just make sure it requires more computational power than anyone could reasonably have.

What is a PRG?

After hearing this rock-paper-scissors story, you propose the following definition:

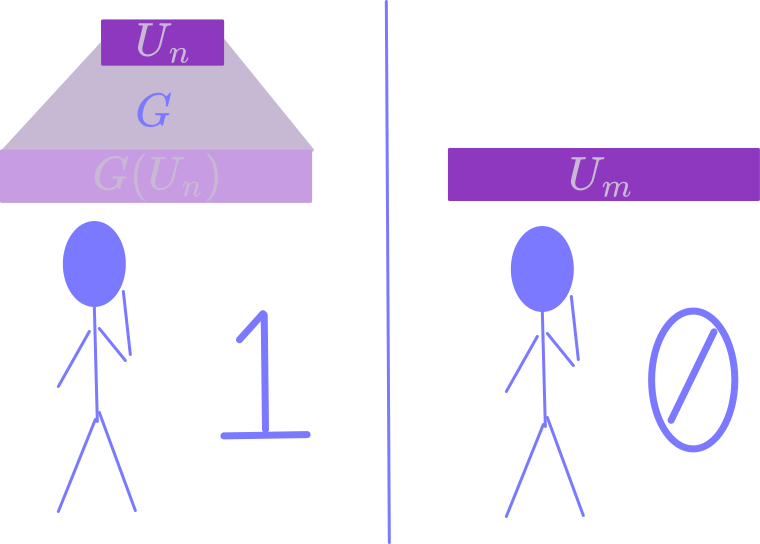
Cryptographic Pseudo-Random Generator (PRG): A function $G:\lbrace 0,1\rbrace^n \rightarrow \lbrace 0,1\rbrace^m$ is a PRG if

It’s computable in polynomial time

It’s length-extending (i.e. $m > n$)

No adversary running in polynomial time can distinguish between $U_m$ and $G(U_n)$ with non-negligible probability, where $U_k$ denotes $k$ uniform random bits.

Illustration of a PRG distinguisher — If an algorithm has different output distributions on $G(U_n)$ vs. real randomness, we say it's a "distinguisher", and $G$ is not a PRG.

When you say “no polynomial-time adversary can distinguish between $U_m$ and $G(U_n)$ with non-negligible probability”, you mean “for any polynomial-time algorithm $\mathcal{A}: \lbrace 0,1\rbrace^m \rightarrow \lbrace 0,1\rbrace$, the acceptance probabilities $\Pr\left[\mathcal{A}(U_m) = 1\right]$ and $\Pr\left[\mathcal{A}(G(U_n)) = 1\right]$ are within $O(1/n^c)$ for any $c$”. This means that, except for with very small (i.e. smaller asymptotically than any inverse polynomial) probability, the behaviours of any polynomial-time algorithm are exactly the same on truly random inputs as opposed to the output of the pseudorandom generator. In particular, this would mean that your rock-paper-scissors opponents can’t beat you more than slightly more than half the time, unless they have a ridiculous amount of computational power.

Of course, the actual reason to care about PRGs is not because of rock-paper-scissors. In the next post, I’ll talk a little about how you can use them to get super cool cryptography stuff like stateless encryption and commitment schemes³. But for this post, I want to answer the question “do these things even exist?”. The answer to that question is “well, for now, it depends on what you’re willing to assume”.

What is a OWF?

Pretty much everything in cryptography is conditional on $\text{P} \neq \text{NP}$. You need to be able to come up with a question where it’s easy to tell that you’ve got the right answer, but hard for anybody else to figure it out. But in order to get interesting things, you usually need even stronger assumptions. Some types of assumptions that tend to get made:

Factoring is hard
There are public-key encryption schemes
There are collision-resistant hash families

One assumption – stronger than $\text{P} \neq \text{NP}$, but weaker than any of those 3 above assumptions⁴ – is the existence of one-way functions:

One-Way Function (OWF): A function $F:\lbrace 0,1\rbrace^n \rightarrow \lbrace 0,1\rbrace^m$ is a OWF if

It’s computable in polynomial time.

No adversary, given an evaluation $y = F(U_n)$ of $F$ on a random input, can produce an element of the preimage (i.e. an $x$ such that $F(x) = y$) with inverse polynomial probability.

Essentially, this is a function that’s easy to compute in one direction, but hard to compute in the other direction. The reason we specify that it’s hard to compute a preimage, as opposed to saying that it’s hard to compute $x$ given $F(x)$, is that if $F$ wasn’t injective there might be so many preimages that it’s super unlikely to get the right one. The reason we say that it’s hard to invert $F$ of a random input, as opposed to a random element of the image, is that maybe some elements of the image can’t be inverted at all. Modular exponentiation is a good example of something that could plausibly be a one-way function: for a given $p$ and $g$, it’s very easy to compute $g^x \text{ mod } p$ given $x$, but we don’t know how to compute $x$ given $g^x \text{ mod } p$ (this is known as the discrete log problem over $\mathbb{F}_p^\times$).

Illustration of a OWF — Given an output of the OWF, you shouldn't be able to find any input mapping to the same value.

The assumption that one-way functions exist turns out to be equivalent to the existence of a whole world of lovely cryptographic tools – Impagliazzo called this world, where one-way functions exist but not stronger things like public-key encryption, Minicrypt, since it’s roughly the minimum we need for the existence of nontrivial cryptography. We’re going to show today that the existence of one-way functions is equivalent to the existence of pseudorandom generators.

Any PRG is necessarily a OWF.

First, I claim that any PRG must also be a OWF – this is the easy direction of the equivalence. Suppose you had a PRG $G$ that wasn’t a OWF. Looking at our definitions, this means there has to exist an algorithm that, given $y = G(U_n)$, produces $x$ such that $G(x) = y$, succeeding with probability $1/n^c$ for some $c$. But, since $m > n$, we know that most strings in $\lbrace 0,1\rbrace^m$ don’t have any preimage under $G$ – definitely our algorithm can’t succeed on those. For any string $y$ in the image of $G$, the probability that $G(U_n) = y$ must be at least $2^{m - n} \geq 2$ times as large as the probability that $U_m = y$. So, the algorithm produces a valid preimage of $y$ at least twice as often when $y$ is drawn from $G(U_n)$ as opposed to $U_m$. We can easily check whether the algorithm has successfully produced a preimage by running $G$ on its output and seeing if it matches the input. So, we’ve shown a way to distinguish between $G(U_n)$ and $U_m$, meaning that $G$ can’t in fact have been a PRG.

Constructing PRGs from OWFs.

The other direction of this equivalence is substantially harder. Having seen the previous claim, you might have some hope that somehow any OWF must be a PRG. But this is just not true. For one, a one-way function doesn’t have to be length-extending, and if something isn’t length-extending it’s definitely not a PRG. But even if it is length-extending, its outputs might not look pseudorandom. For example, if you give me your favourite OWF, I can describe a new OWF that’s “run the old function, and then append 20 1s to the end”. Those 1s won’t make it any easier to invert, but will make it pretty easy to tell outputs of your function from true randomness.

However, it does kinda feel like there’s some pseudorandomness buried somwehere in a OWF. We’ve got a function whose outputs look really complicated (in the sense that nobody can reverse-engineer how we computed them), but is actually pretty easy to compute. In order to build a PRG out of this, we’re going to need to somehow turn that complicatedness into randomness, and then spread out the randomness so it looks uniform. The secret to doing both of these things: hashing! It turns out that just multiplying things by random matrices is kinda op. The basic ideas we need are:

Next-Bit Unpredictability Lemma (for a string to look random, its enough that you can’t predict any bit from the preceding substring)
Goldreich-Levin Theorem (hashing one-way functions with random matrices lets you pull out computationally unpredictable bits)
Leftover Hash Lemma (hashing with random matrices makes high-entropy distributions look uniform)

I’ll go through each of these things, and then walk through how to use them to transform a OWF into a PRG. The original version of this story came from a landmark paper with a lot of beautiful (but kinda messy) probability ideas – there’ve been a number of papers since following the same rough approach, but streamlining aspects of the argument. The version of the story I’m going to follow comes from a recent paper by Pass and Mazor that describes it in terms of sets of unpredictable bits as opposed to pseudoentropy.

Next-Bit Unpredictability

First, let’s talk about a slightly different notion of pseudorandomness. What if, instead of saying “no adversary can distinguish between $U_m$ and $G(U_n)$ with non-negligible probability”, I just said “if a poly-time adversary gets the bits of $G(U_n)$ one-at-a-time, they’ll never be able to predict the next bit with probability much more than 1/2”? This seems like a weaker definition (it’s definitely not stronger – if there was an index where the adversary could predict the next bit with probability better than 1/2, they know that when their prediction is correct the string is more likely to be pseudorandom than truly random) but at least for my rock-paper-scissors story it was all I needed.

It turns out this definition is equivalently strong to full indistinguishibility. The proof of this is what’s called a hybrid argument (or, in the words of somebody in CSAIL whose name I don’t know, “that fancy cryptography term for the triangle inequality”). Suppose your algorithm prints a 1 with probability 50% when given a $100$-bit truly random string, but with probability 51% when given a $100$-bit pseudorandom string. Now, imagine somebody gave you the first 99 bits of a pseudorandom string, but they replaced the last bit with an actual random bit (i.e. they made a “hybrid” of pseudorandomness and real randomness). Does your algorithm behave differently on this distribution versus real randomness? If not, imagine replacing the last 2 bits with real randomness. Is your algorithm more likely to print 1 when the first 99 bits are pseudorandom as opposed to just the first 98? By triangle inequality, there has to be some index $i$ such that the probability of your algorithm outputting 1 is at least .01% more likely when the first $i$ bits are pseudorandom and the last $100-i$ bits are truly random than when the first $i-1$ bits are pseudorandom and the last $100 - (i-1)$ bits are truly random.

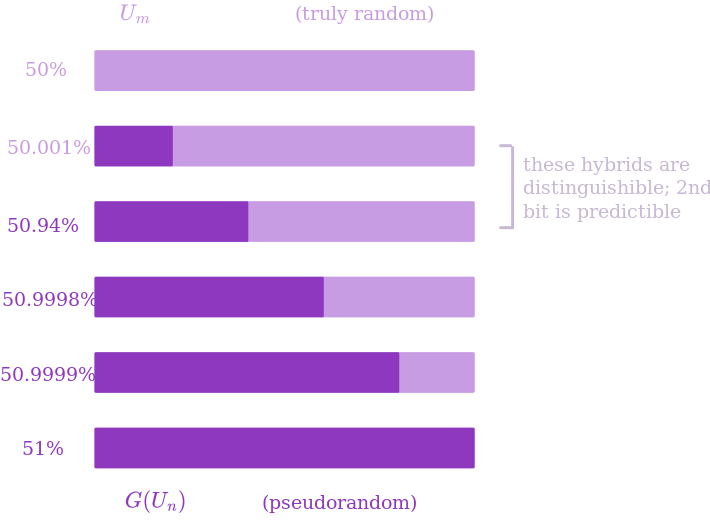
Next-bit unpredictability hybirds — Some pair of adjacent hybrids must be far -- this lets you predict the corresponding bit.

Now, the fact that you can distinguish between those two hybrids also means you can predict the $i$th bit given the first $(i-1)$ with beter than even odds: for both possible values of the $i$th bit, generate the remaining $100 - i$ uniformly at random yourself, then run the distinguisher to see which of these it’s more likely to output 1 on. You’ll get a 1 more often when you chose the right value for the bit, so you have a predictor. This shows that next-bit unpredictability is an equivalent definition of pseudorandomness to the indistinguishability version.

Weaker forms of Next-Bit Unpredictability

Next-bit unpredictability will be a useful way of thinking about pseudorandomness, because it can be relaxed in meaningful ways. Suppose, instead of requiring that every index of the string is unpredictable given the prefix before it, we just require that many indices are unpredictable. Now, if I just told you “indices 13, 26, 42, and 57 are always unpredictable”, maybe this is not too meaningfully different from true unpredictability – it’s equivalent to saying that the string restricted to those indices looks pseudorandom. But it could be the case that the indices where the string looks unpredictable aren’t always the same. For instance, maybe the distribution is such that when the first bit is 1 the next bit is always 1, but when the first bit is 0 the next bit looks totally random. On this distribution, the second bit is sometimes unpredictable (if the prefix before it was 0), but sometimes predictable (if the prefix before it was 1). We want a definition that captures the ways in which such distributions can be “kinda unpredictable”.

Surprising Indices: Given a distribution $\mathcal{X}$ on $\lbrace 0,1\rbrace^n$, we say that $\mathcal{X}$ has $k$ “surprising indices” if, for any predictor $\mathcal{A}$, for $x \gets \mathcal{X}$, there are in expectation at least $k$ indices $i$ such that $\Pr_{y \gets \mathcal{X}}[\mathcal{A}(y_1,\dots, y_{i-1}) = y_i \ | \ y_1, \dots, y_{i-1} = x_1, \dots, x_{i-1}] \approx 1/2$.

This definition is slightly subtle. Of course, once a string is totally fixed there’s nothing unpredictable about it. Here, we say that an index $i$ is surprising for some fixed string $x$ if, given a random output of $\mathcal{X}$, whenever the first $i-1$ bits agree with $x$ the adversary can’t predict the $i$th bit. In our example above, for instance, we would say the second bit is surprising for $x = 011101$, since just knowing that the first bit is $0$ it’s hard to determine the second bit. A distribution has $k$ surprising indices when, for a random $x \gets \mathcal{X}$, we expect that an adversary seeing the string one-bit-at-a-time will have $k$ moments where they really can’t guess the next bit at all.

When the distribution of which indices are surprising is nicely spread-out, we can define a stronger property:

Spread-Out Surprisingness: Given a distribution $\mathcal{X}$ on $\lbrace 0,1\rbrace^n$, we say $\mathcal{X}$ has “spread-out surprisingness” $p$ if, for any index $i$, $\Pr_{x\gets\mathcal{X}}[\text{index } i \text{ is surprising for } x] \geq p$.

In our construction of a PRG, we’ll first construct a distribution with many surprising indices, then turn that into one with lots of spread-out surprisingness, and then finally turn that into something fully pseudorandom. To get surprising indices from OWFs, we’ll need the Goldreich-Levin Theorem.

Goldreich-Levin Theorem

The definition of a OWF tells us that, given $f(x)$, it’s hard for any algorithm to find something in the preimage. Is it hard to find, say, just the first bit of $x$? Well no, not necessarily – for example, imagine $f(x)$ really just keeps the first bit of $x$ as is, and just applies some crazy function to all the other bits. This might well be one-way because the rest of the bits are hard to figure out, but it’s pretty easy to figure out the first bit of the input.

Well, is there any 1-bit function $g(x)$ that’s hard to compute given $f(x)$? Of course, if $f$ is losing information, it might be kinda trivially hard to compute $g(x)$ – supposing, say, that $f$ doesn’t even look at the first bit of the input, there’s definitely no way to compute the first bit of $x$ from $f(x)$. But if we can find a $g$ that’s hard to predict for computational reasons, we’d be in business – seems like we’re generating some new unpredictablity that wasn’t there before. Such a function is called a “hardcore predicate”, and the Goldreich-Levin theorem says that we can modify any one-way function to get one with hardcore predicates.

Illustration of a band called the Hardcore Predicates — I'm not gonna let the MAN figure out the dot product of $x$ with a random bitvector!

The idea is: taking your original function $f(x)$, modify it to be $f’(r,x) = (r,f(x))$. That is, $f’$ now takes an additional $n$ bits of input, which it just outputs unchanged. Goldreich-Levin says that the function $g(r,x) = \langle r, x \rangle$ – i.e. the inner product – is a hardcore predicate for $f’$. In other words, the dot product of $x$ with a random vector $r$ is unpredictable given $f(x)$ and $r$.

Rough proof sketch that this is hardcore: suppose we had an algorithm with good odds of guessing $\langle r , x \rangle$ given $f(x)$ and $r$. Then, there’s a decently large fraction of $x$’s such that we have good odds over $r$ of guessing $\langle r, x \rangle$ for those specific “good” $x$’s – let’s imagine we’re dealing with one of those. We could choose $n$ random values $r_1, \dots, r_n$ ourselves, and run our algorithm to figure out $\langle r_i, x\rangle$ and $\langle r_i \oplus e_i, x\rangle$ for all $i$, where $e_i$ is the $i$th standard basis vector. Since $r_i$ and $r_i \oplus e_i$ are both uniformly distributed on their own, there’s a good chance (if we repeat things for error reduction, then appeal to Chebyshev) that we’ll compute all those dot products correctly, and then will just be able to read off $x$. This would give an algorithm capable of inverting $f$ on a large fraction of $x$’s with good probability, which breaks one-wayness. I was a little careless here, though, because this requires that the probability of getting both $\langle r_i, x\rangle$ and $\langle r_i \oplus e_i, x\rangle$ correct is more than $1/2$, but we actually only know that we’re right on each one individually with probability more than $1/2$, so we might have probability close to $1/4$ of guessing both simultaneously correct. The solution to this problem is to choose the $r_i$s, instead of as $n$ independent random strings, to be generated by a small number of random “seeds” (i.e. each of the $r_i$s is the sum over a different subset of our $O(\log n)$ many random seed vectors). This construction still maintains pairwise independence, which is all you actually need for Chebyshev, but now all possible values of the $\langle r_i, x\rangle$ s can be brute force enumerated over, since we can try all values of the dot products with the seeds. (Don’t worry if you didn’t super follow this – I cut a good amount of details. Worth looking up a more verbose proof if you haven’t seen this before. Or don’t bother with the details – they’re not important for this construction.)

Leftover Hash Lemma

The other tool we’ll need is the Leftover Hash Lemma⁵. The leftover hash lemma is a statement about randomness extraction: given a distribution that’s not necessarily uniformly random, but does have high entropy, can we turn it into one that’s close to uniform? As long as we’re willing to add in some truly uniform randomness on top⁶, this turns out to be possible! As with most things in life⁷, it can be solved with hashing.

We say that a distribution $\mathcal{X}$ has high min-entropy (denoted $H_\infty(\mathcal{X})$) when the probability of any element of the range is small. Specifically, if $p_{\max}$ is the probability of the most likely element in $\mathcal{X}$, $H_{\infty}(\mathcal{X}) = - \log p_{\max}$. Note that high min entropy is necessary for extraction – high Shannon entropy is not enough (we could have for instance a distribution with high Shannon entropy that outputs $1$ with 99% probability, but then is uniform over a very large range the other 1% of the time; this is not good enough to extract from).

We say that a family of functions, parameterized by a “key” $k$, is a 2-universal hash family if, for any two distinct elements $x$ and $y$ of the domain, the probability over $k$ that $h_k(x) = h_k(y)$ is the same as it would be if $h_k$ was a random function (i.e. 1 over the size of the codomain). For the purposes of this post, we’ll only need to think about the case when the hash family consists of multiplication by a random matrix over $\mathbb{F}_2$, in which case it’s not hard to see we have this property.

Now, we can state the Leftover Hash Lemma as follows:

Leftover Hash Lemma: For any distribution $\mathcal{X}$, and any 2-universal hash family $\lbrace h_k: \lbrace 0,1\rbrace^n \to \lbrace 0,1\rbrace^{m}\rbrace$, if $m \leq H_\infty(\mathcal{X}) - 100 \log(n)$ then the distribution of the pair $(k, h_k(x))$ is statistically close to uniform.

To prove this lemma, we first note that $(k, h_k(x))$ has collision probability close to that of uniform randomness, which then implies closeness of the distributions in $\ell_2$ distance, which gives closeness in statistical distance. More details about extraction and the LHL can be found in these nice notes by Salil Vadhan.

Finding many surprising indices

Ok, now that we have this machinery, the construction of PRGs from OWFs will actually not be too difficult. As a warm-up let’s imagine that $f$ is not just a one-way function, it’s actually a one-way permutation (i.e. it’s a bijection $\lbrace 0,1\rbrace^n \to \lbrace 0,1\rbrace^n$). In this case, we can turn $f$ into a PRG just by applying the Goldreich-Levin Theorem – we let $G(r, x) = (r, f(x), \langle r, x \rangle)$. The first $2n$ bits of $G$’s output are totally uniform, and then the last bit is computationally unpredictable from the previous bits, so by the equivalence of next-bit unpredictability and indistinguishability $G(U_{2n}) \approx U_{2n+1}$. This is very nice, but it relied pretty heavily on $f$ being a permutation, and the existence of one-way permutations is not known to be implied by the existence of general one-way functions. It’s gonna take us a little more elbow grease to get PRGs from just OWFs. (We can and will assume, though, that $f$ goes from $\lbrace 0,1\rbrace^n \to \lbrace 0,1\rbrace^n$. This is without loss of generality – if its domain is smaller, pad it with some dummy bits we don’t even look at, and if its codomain is smaller pad it with 1s.)

Well, let’s suppose now that instead of being a one-way permutation, we just know that $f$ is $r$-regular, in the sense that every element in the image has between $2^{r-1}$ and $2^{r}$ preimages. The tools we mentioned above give us the following two facts:

If we multiply $f(x)$ by a random $(n - r - 100 \log n) \times n$ binary matrix $M_1$, the joint distribution of the matrix and the product looks statistically uniform. This follows directly from the Leftover Hash Lemma: $f$ being $r$-uniform is equivalent to $f(x)$ having min-entropy $n - r$.
If we multiply $x$ by a random, $(r + 200 \log n) \times n$ binary matrix $M_2$, the joint distribution of $M_2$ and $M_2x$ looks computationally unpredictable, even given $f(x)$. This is a little less obvious, but does follow from Goldreich-Levin. The idea is: suppose there was some index $i \in [r + 200 \log n]$ such that an efficient adversary had a decent (i.e. inverse polynomially more than $1/2$) shot at predicting the $i$th bit of $M_2 x$ given $M_2$, $f(x)$ and the previous $i-1$ bits of $M_2 x$. Now, we want to use this to break the one-way function – i.e. we’re given $f(x)$ and want to compute something in the preimage. To do so, we choose the first $i-1$ rows of $M_2$ randomly ourselves, then randomly guess the first $i$ bits of $M_2x$. The chance that we guess all of them right is only $2^{-i} \geq 2^{- r - 100 \log n} = \frac{1}{\text{poly}(n)} \cdot 2^{-r}$ – but if we did get all of them right, now when we choose the next row $v$ at random we have an (inverse polynomial) advantage in predicting $\langle v, x \rangle$, which Goldreich-Levin says gives us a good (inverse polynomial) chance of determining $x$. So, with probability $\frac{1}{\text{poly}(n)} \cdot 2^{-r}$, we’re able to determine $x$ given $f(x)$. But now, notice that since $f$ is $r$-regular, there’s at least $2^{r-1}$ different values in the preimage of $f(x)$ – since we’ve guaranteed that our algorithm returns each of them with probability $\frac{1}{\text{poly}(n)} 2^{-r}$, this means that our algorithm returns some preimage with probability $\frac{1}{\text{poly}(n)}$. Take that, so-called one-way function!

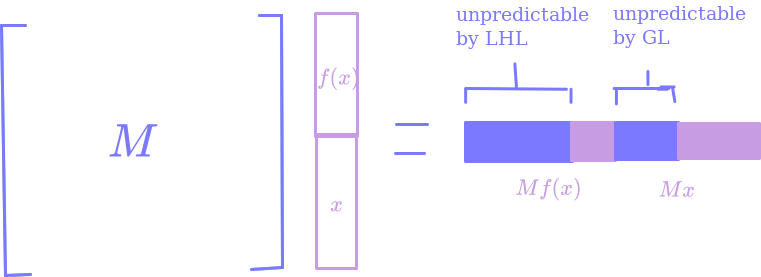
Ok, what is this telling us? Well, consider the function $G: \lbrace 0, 1\rbrace^{n \times n} \times \lbrace 0,1\rbrace^n \to \lbrace 0, 1\rbrace^{n \times n} \times \lbrace 0,1\rbrace^n \times \lbrace 0,1\rbrace^n$, $G(M, x) = (M, Mf(x), Mx).$

If we feed $G$ a random input, I claim that the output is going to have more than $n^2 + n$ surprising indices – we’re making some pseudorandomness! The first $n^2$ indices are definitely surprising, since they’re uniformly random. The next $(n - r - 100 \log n)$ indices are statistically close to uniform, and hence surprising⁸, by our first point. Then, since seeing $M$ and $Mf(x)$ at most tells you $M$ and $f(x)$, our second point guarantees that the first $(r + 200 \log n)$ indices of $Mx$ are surprising. So, overall we have $n^2 + n + 100 \log n$ surprising indices – more than the amount of randomness we fed in.

Illustration of the surprising indices — Between Goldreich-Levin and the Leftover Hash Lemma, we get a lot of surprising indices.

Well, what if $f$ wasn’t $r$-regular? Turns out this is not a big deal, since we did the same construction no matter what $r$ was. Just imagine breaking up the domain $\lbrace 0,1\rbrace^n$ into $n$ different chunks based on how many preimages their image has – so that $f$ is $1$-regular on the first chunk, $2$-regular on the second chunk, etc. We can forget about all the chunks that represent less than a polynomial fraction of the domain – they essentially never come up. For every chunk that does make up a polynomial fraction of the domain, we must have that $f$ restricted to that chunk is one-way⁹. Thus, $f$ restricted to that chunk is a regular OWF, so by the above argument, $G$ has $n^2 + n + 100 \log n$ surprising indices conditioning on its output being in the image of that chunk. Since this is true on every chunk, $f$ has $n^2 +n + 100\log n$ surprising indices in general.

Spreading out the surprise

Alright, we’re cooking here. We have a function where we can feed in some random bits, and get an output with more surprising indices than the number of bits we fed in. In order to use this to get a PRG, though, it’s not going to be enough to have a large number of surprising indices in expectation – we’d really like for each individual index to be surprising with reasonably good probability. To do this, we’ll just randomly shift things!

Let’s apply our $G$ from above to $n$ different $n$-bit inputs $x_i$. Note that our surprisingness guarantees still hold when if we use the same random matrix $M$ for each of these copies of $G$, so for simplicity let’s do that. Alright, now we’ve got (in addition to our random $M$), a $2n^2$-bit string $(Mf(x_1), Mx_1, Mf(x_2), Mx_2, \dots, Mf(x_n), Mx_n)$. In order to make it so that every index of this string has the same probability of being surprising, we can pick a random $i \in [2n]$, and then truncate the first $i$ and last $n-i$ bits, reducing the string to length $2n^2 - 2n$. This shift ensures that, even if some indices of $G’$ are less likely to be surprising than others, in the final construction all indices are equally likely. We now have a function $G’: \lbrace 0,1\rbrace^{n\times n} \times [n] \times \lbrace 0, 1\rbrace^{n \times n} \to \lbrace 0,1\rbrace^{n\times n} \times \lbrace 0,1\rbrace^{2n^2 - n}$, $G’(M, i, (x_1, \dots, x_n)) = (M, (Mf(x_1), Mx_1)[i:], (Mf(x_2), Mx_2), \dots (Mf(x_{n-1}), Mx_{n-1}), (Mf(x_n), Mx_n)[:n-i]).$

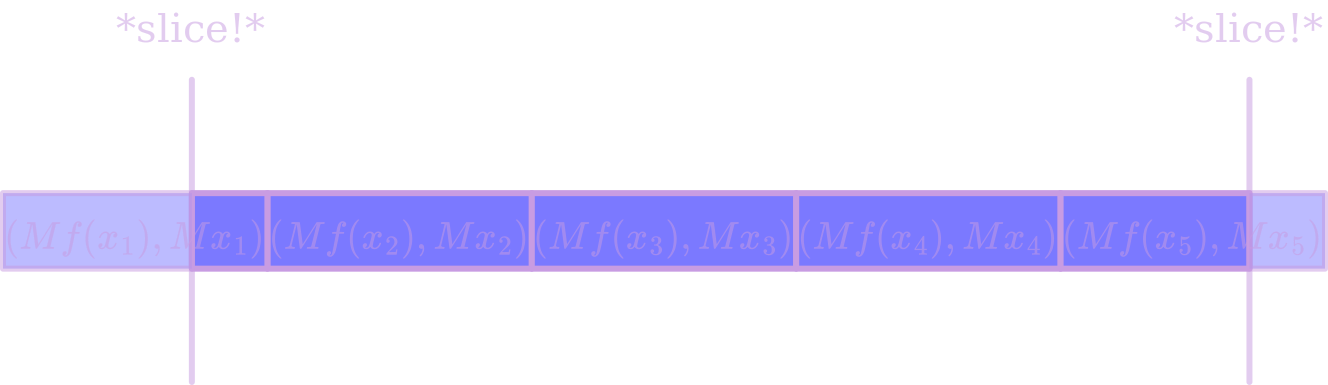
Chop chop! — No matter how the surprisingness distribution looked within each block, now it's all spread out.

We feed in $2n^2 + \log n$ random bits ,and the number of surprising indices is $n^2 + (n-1)(n + 100 \log n) \geq 2n^2 + 80 \log n$, so, we’re still amplifying the surprisingness. But now, it’s mixed together a little more evenly – for any index of the output (except for $M$, which we’ll just append separately because it’s already totally uniform), the probability that index is surprising is $\frac{ (n-1)(n + 100 \log n)}{2n^2 - n} = \frac{1}{2} + \frac{50 \log n}{n}$. Our entropic dough has risen beautifully; it’s time to take it out of the oven, slice it up, and enjoy!

Shlopping the entropy together

Alright, you ready for this point in the construction? This is gonna require some kinda crazy stuff, probably unlike anything you’ve ever seen before.

Just kidding. We’re gonna hash with random matrices again :)

The construction will be: compute $G’$ $n^3$ times on different random inputs¹⁰, and arrange the outputs as the rows of an $n^4 \times (2n^2 - n)$ matrix. Now, let $H$ be a random $n^3 \times (n^3/2 + 10 n^2 \log n)$ matrix, which we’ll use to hash all the columns of this matrix. That is, we output first $H$ applied to all the first entries of the matrix, then $H$ applied to all the second entries, etc, for a total of $(n^3/2 + 10 n^2 \log n)(2n^2 - n) \geq n^5 + n^4 \log n$ output bits. The total number of bits we fed in (not counting the hash functions, since we’ll just output them verbatim on top of this) was $n^5 + n^3 \log n$. So, we’re length extending!

Hashing columns — We output the hashes of each column in order.

The question now is: how do we know this output is computationally indistinguishable from uniform? There’s a couple steps in this argument.

Recall that indistinguishability is equivalent to next-bit unpredictability at every index. So, it suffices to show that no algorithm can predict the hash of one column given the hashes of all the previous columns.
Choose some column of the matrix. For how many rows of the matrix is that column one of the surprising indices? Well, each row is surprising on that column with probability $\frac{1}{2} + \frac{50 \log n}{n}$, so in expectation we’ll have $n^3/2 + 50 n^2 \log n$ of them. But also, since rows are generated indendently, these are independent events – Chernoff bounds tell us that, except for with exponentially small probability, the count will be square-root concentrated around the mean. So, except with exponentially small probability, every column will have at least $n^3/2 + 10 n^2 \log n$ surprising entries.
Now, imagine we replaced one of the bits corresponding to a surprising index on that column with an actual uniform random bit. Could an adversary, looking at just that column and the previous ones, tell the difference? Well, no – this is what surprising means! If an adversary could tell the difference, then by setting up the rest of the matrix ourself we could use that adversary to predict the surprising entry on that row¹¹. Repeating this argument, we can replace every surprising index in the column with actual uniform random bits, and the adversary must have the same probability of being able to predict the hash of the column.
But oh, wait, now this column has $n^3/2 + 10 n^2 \log n$ of its entries uniformly random – so, the column has min entropy at least $n^3/2 + 10 n^2 \log n$. By the leftover hash lemma, the hash of the column is statistically close to uniform! I’d like to see an adversary predict that. 😎

For next time

Ok, that’s it! We’ve built PRGs from nothing but OWFs. Having PRGs will in turn open up a wonderful world of crypto – from stateless symmetric-key encryption and message authentication to commitment schemes.

Let me know if you liked this post! Are there things you think I should change? You can’t leave comments because idk how to set that up, but you should all press ctrl-shift-i on your keyboards, add an extra little “<div>” at the bottom, type up a response there, and then mail a screenshot to Nathan Sheffield at Cambridge MA. If your comments elicit any kind of emotional response, such as can be expressed by an emoticon, I will draw one and return the letter to you within 14 business days.

Yours truly, forever and always, Nathan

Assuming you don’t have some physical tells that let them see what you’re planning to do. ↩
I was about to say “natural” here, but had to stop myself because this is like the most contrived thing ever. ↩
The kinds of parameters crypto people usually talk about PRGs with are not the only parameters you could set. Here, we’re just thinking about PRGs that can fool any polynomial-time algorithm, and that produce at least one more random-looking bit than you put in (which we can then extend to get polynomially more random bits – more on this next time). What complexity theory like, though, is to try and see if you can fool all algorithms with any specific polynomial runtime, but with a random seed smaller than polynomial. That is, suppose for any $c$, you could get an $n^{500 c}$-time PRG with seed length $\log n$ such that no $n^c$-time algorithm can tell the difference. This would be super cool, because then we could learn the average behaviour of the algorithm just by enumerating all possible seeds, and so we’d know that $\text{P} = \text{BPP}$. ↩
In the sense that any of those 3 assumptions would imply the existence of OWFs, but none of them are known to be equivalent. ↩
Not to be confused with the Leftover Hash-Browns Lemma, which says that it’s a good idea to make extra mashed potatos and then fry the remainder the next morning with breakfast. ↩
This is necessary – you can’t have a truly deterministic extractor for arbitrary sources of high min-entropy. However, if you restrict to only a specific class of $\mathcal{X}$, it’s sometimes possible to get deterministic extraction. ↩
@Alek Westover endorses this message. (Also, you should check out Alek’s blog here!) ↩
Ok, I’m glossing over things a little bit – you might be worried that I only claimed I was $n^{-100}$-close to uniform. Well, just increasing $100$ to be bigger than your favourite constant shows that this is arbitrarily polynomially close to uniform. If you claim any particular inverse polynomial statistical distance, I can find an algorithm with a corresponding inverse polynomial chance of inverting the OWF by our Goldreich-Levin argument. ↩
If we have inverse polynomial probability of inverting conditional on the input being in that chunk, we also have inverse polynomial probability of inverting in general. ↩
Those of you who actually use computers may ask “shoot is $n^3$ really necessary here?” To which I respond both (a) No – according to Mazor and Pass I could have said $n^2 / \log^2 n$ or something, but I was just sloppy. (b) Pretty sure nobody actually does this irl anyway. They just take functions that look pretty complicated, see if anyone can break them, and if not say “yep looks pseudorandom”. Or the NSA promises you something is definitely totally a PRG, and you believe them because why would those guys lie to you? ↩
If you’re being careful, you’ll notice that, in order to actually use this to get a predictor, we need the ability to predict which bits are supposed to be surprising, which might not be easy to figure out just by looking at the OWF. But, if we had a non-uniform algorithm (i.e. a circuit as opposed to a Turing machine), we could just hardwire this information about the OWF. So this argument only gives a PRG if we assume the OWF was secure against non-uniform adversaries – it’s possible to get security against uniform adversaries too, but a little more work. ↩